I love Mathematics (and that is not going to help my blog’s engagement) Either way, I’m a willing fan of finding mathematical solutions to general problems.
Now if you’ve solved problems on platforms like Codechef or LeetCode, you’d have come across problems tagged with “Union Find” or “Disjoint Set”. Let’s understand what that is about.
The Problem
Consider an undirected graph with nodes numbered from 0 to n-1. Given a source, and a destination node, you’re tasked with finding if there exists a path, on the graph, between the two.
The Math of it all
What are Disjoint Sets?
Sets having no common data i.e. considering three sets A(5,6,7), B(5,8,9) and C(1,2,4), it’s important to realize that A and C are disjoint sets, while A and B are not.
What this also means is that most problems involving non-overlapping values of data can be solved using disjoint sets.
Underlying Philosophy
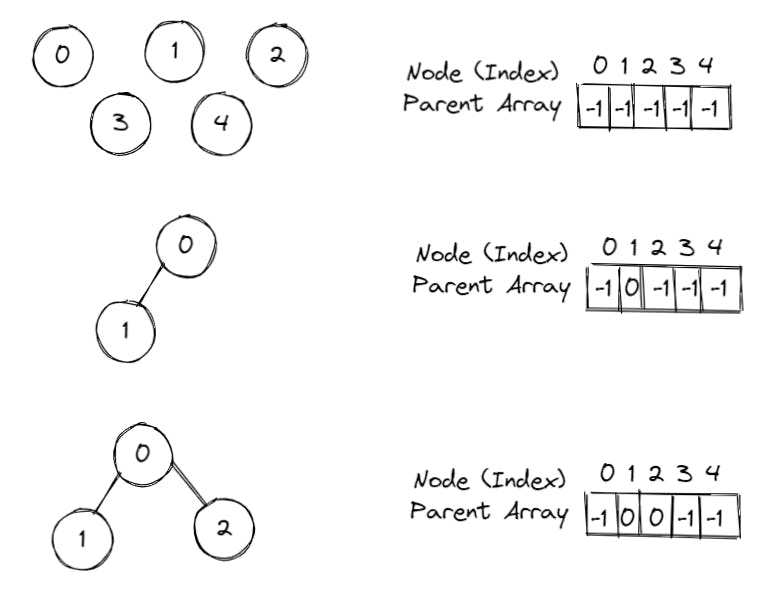
Working with disjoint sets through code can be simplified by visualizing set data in the form of a tree, with children, their respective roots and an absolute root for the entire structure.
The working logic for any problem that we’ll solve this way, is that elements/nodes belonging to the same tree, also belong to the same set.
Let’s visualize the tree and store its values using an array where the nodes are used as an index, and the array contains values of parents against those nodes.

The Find() Function
This function is supposed to help us find the absolute parent root of any given element. This is a recursive relation that keeps on searching for the root index until ParentArray[index] becomes equal to -1.
In the above example, if we need to find the root of say, 3, the code establishes that 2 is the parent of 3, but 2 is not the final answer since it is not an absolute parent root (its parent is not -1). So, it continues the operation until it reaches 0.
The Union() Function
This is where all the real work is being done. This method reads the graph from the input and then forms sets accordingly.
In the question itself, we might not be provided with the whole graph, usually, only edges are given. This method is used to traverse those edges and form the required connections on the graph, or the required sets in this case.
It takes in two vertices and checks if they have the same absolute parent, i.e if they are already connected. If yes, it continues to the next iteration while in an opposite scenario, it forms a union operation on the two vertices.
Initially, in the unmade graph, we consider that all the vertices are single nodes and are logically their absolute parents. We begin performing a union operation according to the given edges as follows.
The Problem
Now that we’ve connected the graph, let’s try to break the problem into pieces.
Suppose we need to find if a path exists between node 4 and node 3, unequivocally, we need to check if within the given data, set (4,3) is present or not.
i.e. if 4 and 3 belong to the same set
i.e. 4 and 3 belong to the same tree
i.e. 4 and 3 have the same absolute parent
This can be achieved by simply calling the find function on the given vertices, storing them in separate variables and returning true or false if their absolute parent roots match, and don’t match respectively.

Wrapping Up
The first thing to consider solving any similar problem is to check if the question involves Directed Graphs. DSU can only be applied to undirected graph problems i.e. in situations where the directionality of the graph is not determined by the given edges.
